Unitér csoport
Ma a Unitér csoport olyan téma, amely nagy érdeklődést és vitát vált ki a társadalomban. A Unitér csoport évek óta a különböző területeken dolgozó szakértők és tudósok tanulmányozásának, elemzésének és elmélkedésének tárgya. Relevanciáját számos tanulmány, konferencia és publikáció tükrözi, amelyek célja, hogy megértsék hatását és hatókörét különböző összefüggésekben. A Unitér csoport olyan téma, amely határokon átível, és különböző korú, nemű, kultúrájú és nemzetiségű embereket ér el, gazdagító párbeszédet generálva, amely lehetővé teszi, hogy különböző nézőpontokból megértsük. Ebben a cikkben elmélyülünk a Unitér csoport világában, feltárva annak eredetét, fejlődését és következményeit a mai társadalomban. Interjúk, elemzések és tanúságtételek révén hangot adunk azoknak, akikre hatással volt a Unitér csoport, és elmélyülünk annak globális következményeiben.
Az unitér csoport, jelölés szerint a matematikában az unitér mátrixok csoportja, melynek asszociatív csoportművelete a mátrixszorzás. Az unitér csoport részcsoportja az általános lineáris csoportnak (). Az fontos részcsoportja a speciális unitér csoport , amely olyan unitér mátrixokat tartalmaz, melyeknek determinánsa egy.
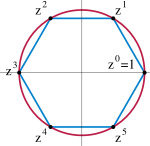
A legegyszerűbb unitér csoport az , amely megfeleltethető a körcsoportnak, az egységhosszúságú komplex számok csoportjának. Az csoport elemei tehát ábrázolhatók a komplex sík egységkörén.
Az unitér csoport egy -dimenziós valós sima sokaság, amelyben a mátrixszorzás tetszőlegesen sokszor differenciálható, ezért egy Lie-csoport. A csoport Lie-algebrája az antihermitikus mátrixok algebrája, ahol a Lie-zárójel a mátrixok kommutátora.
Tulajdonságai
Mivel egy unitér mátrix determinánsa egy egységhosszúságú komplex szám, a
egy csoporthomomorfizmus, melynek magja pontosan . Ennek következtében
Lie-csoportok rövid egzakt sorozata. Az abban az értelemben tekinthető részcsoportjának, hogy olyan diagonális mátrixok ábrázolják az elemeit, amelyeknek első eleme , a többi eleme pedig 1. Ennek következtében felírható az és féldirekt szorzataként.
Az unitér csoport csak esetén kommutatív. A Schur-lemma következtében az csoport centruma az alakba írható mátrixok halmaza, ahol és az egységmátrixot jelöli. Az centruma tehát izomorf a csoport egy egydimenziós kommutatív normálosztójához (-hez), így az unitér csoport reduktív csoport.
Topológia
Az unitér csoport részhalmaza -nek, az komplex mátrixok halmazának, amely homeomorf a -dimenziós euklideszi térhez. Az unitér csoport, felruházva részhalmazaként az altér-topológiával, egy topologikus teret alkot, amely kompakt és összefüggő. Az összefüggőség abból következik, hogy bármely unitér mátrix diagonalizálható egy unitér mátrixszal, a sajátértékei pedig egységhosszúságú komplex számok, tehát
Mivel a csoport egységelemét és egy tetszőleges -t összeköti egy út, ezért útszerűen összefüggő, tehát összefüggő. Azonban az unitér csoport nem egyszeresen összefüggő, ugyanis a fundamentális csoportja izomorf -vel.[1] Ez a tulajdonság abból látható, hogy felírható és féldirekt szorzataként, így az unitér csoport fundamentális csoportja megfeleltethető és fundamentális csoportjainak Descartes-szorzatával. A speciális unitér csoport egyszeresen összefüggő, tehát a fundamentális csoportja triviális, míg az egydimenziós unitér csoport topológiailag egy kör, amelynek fundamentális csoportja izomorf -vel. A determináns indukálja a fundamentális csoportok izomorfizmusát.
Az unitér csoport Weyl-csoportja a szimmetrikus csoport .
Jegyzetek
Fordítás
Ez a szócikk részben vagy egészben az Unitary group című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Források
- Hall, Brian C.. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, 2nd, Graduate Texts in Mathematics, Springer (2015). ISBN 978-3319134666