Teljes páros gráf

Teljes páros gráf
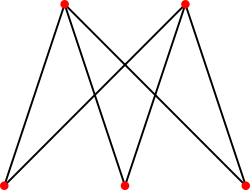K3,2
Névadó	Kazimierz Kuratowski
Csúcsok száma	n + m
Élek száma	mn
Sugár	${\displaystyle \left\{{\begin{array}{ll}1&m=1\vee n=1\\2&{\text{különben}}\end{array}}\right.}$
Átmérő	${\displaystyle \left\{{\begin{array}{ll}1&m=n=1\\2&{\text{különben}}\end{array}}\right.}$
Derékbőség	${\displaystyle \left\{{\begin{array}{ll}\infty &m=1\vee n=1\\4&{\text{különben}}\end{array}}\right.}$
Kromatikus szám	2
Élkromatikus szám	max{m, n}
Automorfizmusok	${\displaystyle \left\{{\begin{array}{ll}2m!n!&n=m\\m!n!&{\text{különben}}\end{array}}\right.}$
Jelölés	${\displaystyle K_{m,n}}$

A teljes páros gráf olyan páros gráf, ahol mindkét partíció minden csúcsára fennáll, hogy vezet belőle él a másik partíció minden csúcsába. A teljes k-részes gráf speciális esete, ahol k=2.

Teljes páros gráfnak nevezünk valamely ${\displaystyle G=(V_{1}+V_{2},E)}$ páros gráfot, ha bármely ${\displaystyle v_{1}\in V_{1}}$ és ${\displaystyle v_{2}\in V_{2}}$ csúcspárra létezik ${\displaystyle \{v_{1},v_{2}\}\in E}$ él.

${\displaystyle K_{m,n}}$ szimbólummal jelöljük azt a teljes páros gráfot, ahol ${\displaystyle \left|V_{1}\right|=m}$ és ${\displaystyle \left|V_{2}\right|=n}$. A jelölés Kazimierz Kuratowski lengyel matematikus nevét őrzi.

• a ${\displaystyle K_{m,n}}$ gráf ${\displaystyle m+n}$ csúcsot és ${\displaystyle m\cdot n}$ élt tartalmaz
• a Kuratowski-tétel szerint síkbarajzolható gráf nem tartalmazhat a ${\displaystyle K_{3,3}}$ gráffal topologikusan izomorf részgráfot.
• a definíció következményeként ${\displaystyle K_{m,n}=K_{n,m}}$
• a ${\displaystyle K_{m,n}}$ gráf összefüggő
• élgráfjai bástyagráfok
• csillagkromatikus száma ${\displaystyle \chi _{s}(G)=min(m,n)+1}$.^[1]

Egy K_m,n teljes páros gráf akkor és csak akkor körmentes, ha m=1 vagy n=1. Ilyen esetben lehet beszélni csillaggráfról (illetve csillagtopológiáról):

• 
  S₃ = K_1,3
• 
  S₄ = K_1,4
• 
  S₅ = K_1,5
• 
  S₆ = K_1,6

Speciális jelentősége van még a gráfok síkbarajzolhatóságában a K_3,3 gráf (három ház–három kút-gráf):

• 
  K_3,3

Ha m=n, akkor a gráf csúcstranzitív.

• Páros gráf
• Teljes gráf

• Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, p. 17, ISBN 3-540-26182-6, <http://diestel-graph-theory.com/index.html>.
• Bondy, John Adrian & Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, p. 5, ISBN 0-444-19451-7, <http://www.ecp6.jussieu.fr/pageperso/bondy/books/gtwa/gtwa.html>. Hozzáférés ideje: 2010-04-04 Archiválva 2010. április 13-i dátummal a Wayback Machine-ben